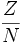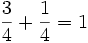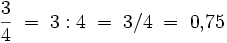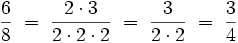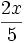Begriffe und Wiederholung

Bruchrechnung

aus Wikipedia, der freien Enzyklopädie

(Weitergeleitet von Bruchrechnen)

Ein Kuchen ist in vier gleiche Teile geteilt. Jeder Teil des Kuchens entspricht 1⁄4. Wie man sieht, entsprechen zwei Teile (2 x 1⁄4 = 2⁄4) einem halben (=1⁄2) Kuchen.

Ein Kuchen ist in vier gleiche Teile geteilt. Jeder Teil des Kuchens entspricht ¹⁄₄. Wie man sieht, entsprechen zwei Teile (2 x ¹⁄₄ = ²⁄₄) einem halben (=¹⁄₂) Kuchen.

Definition und Bezeichnungen

Brüche werden im Allgemeinen durch eine Übereinanderstellung von Zähler und Nenner, getrennt durch einen waagerechten Strich, dargestellt:

$\frac{Z}{N}$

der Zähler Z ist dabei der Dividend der Division, der Nenner N ist der Divisor. Jede Division lässt sich als Bruch schreiben.

Zähler und Nenner einer konkreten Bruchzahl sind ganze Zahlen. Dabei darf der Nenner niemals Null sein, da eine Division durch Null nicht definiert ist (und sich nicht sinnvoll definieren lässt).

Ist der Zähler in einem Bruch 1 (z. B. 1/2 oder 1/9), spricht man von einem Stammbruch, alle anderen sind abgeleitete oder Zweigbrüche.

Wenn bei Zweigbrüchen der Betrag des Zählers kleiner als der des Nenners ist, so handelt es sich um echte (eigentliche) Brüche (z. B. 6/7 oder 2/5), andernfalls von unechte (uneigentliche) Brüche (z. B. 7/6 oder 11/3).

Im Alltag schreibt man auch gemischte Brüche, also den ganzzahligen Anteil, d. h. die zur Null hin gerundete Zahl, und anschließend den Divisionsrest (kurz Rest) als echten Bruch, zum Beispiel 1½ statt 3/2. In manchen Ländern wie Frankreich sind gemischte Brüche unüblich.

Beispiele für Brüche

$\frac{3}{4} + \frac{1}{4} = 1$
Man liest: "drei Viertel plus ein Viertel "

$\frac{2}{3}$

der Bruch mit der 2 im Zähler und der 3 im Nenner bedeutet "zwei Drittel", also zwei Teile eines in drei gleichgroße Teile geteilten Ganzen.

$\frac{3}{4}$

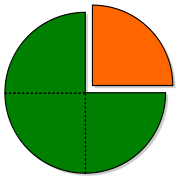
bedeutet entsprechend "drei Viertel".

Das bedeutet, dass "ein Ganzes" aus "drei (gleich großen) Dritteln", und im zweiten Beispiel aus "vier (gleich großen) Vierteln" usw. besteht. Somit wird klar, dass man einen Bruch auch als eine Division auffassen kann.

$\frac{3}{4} \; = \; 3 : 4 \; = \; 3 / 4 \; = \; 0{,}75$

Kürzen von Brüchen

Brüche können gekürzt werden, wenn Zähler und Nenner mindestens einen gemeinsamen ganzzahligen Teiler haben. Dabei ist es hilfreich, wenn man den Zähler und den Nenner in ihre Primfaktoren zerlegt.

Eine weitere gute Erklärung zum Kürzen von Brüchen findest du hier.

$\frac{6}{8} \; = \; \frac{2 \cdot 3}{2 \cdot 2 \cdot 2} \; = \; \frac{3}{2 \cdot 2} \; = \; \frac{3}{4}$

Erweitern von Brüchen

Erweitern eines Bruches bedeutet, dass man den Zähler und den Nenner des Bruches mit der gleichen Zahl (aber nicht mit 0) multipliziert. Der Wert des Bruches bleibt dabei gleich. Die Zahl, mit der man erweitert, wird als Erweiterungsfaktor bezeichnet.

So kann beispielsweise $\frac{2}{3}$ auf $\frac{4}{6}$ erweitert werden.

Zähler (oben) und Nenner (unten) wurden in diesem Beispiel jeweils mit dem Faktor 2 multipliziert: $\frac{2*2}{3*2}$ = $\frac{4}{6}$

Auch Ausdrücke, die Variablen enthalten, kann man als Bruch schreiben:

$\frac{2x}{5}$

bedeutet "zwei x geteilt durch Fünf".

Der Beitrag ist lizenziert unter derGNU Free Documentation License. Quelle:Artikel "Bruchrechnen".

« Vorheriges | Nächste »